Burnling's Blog
0%

tarjan

发表于 更新于

亿些概念

  • 强连通：对于有向图中两点 $i,j$ ,若存在 $i$ 到 $j$ 和 $j$ 到 $i$ 的路径，则称 $i$,$j$ 强连通

    弱连通：对于有向图中两点 $i,j$ ,若存在 $i$ 到 $j$ 或 $j$ 到 $i$ 的路径，则称 $i$,$j$ 弱连通

  • 强连通图：任意两点均强连通的图

    弱连通图：任意两点均弱连通的图

  • 强连通分量：有向图的极大强连通子图

  • 割点：删去这个点，图的联通块个数增加

    桥：删去这条边，图的联通块个数增加

  • 点连通度：最小的点数使得删去之后图不连通
    边连通度：最小的边数使得删去之后图不连通

  • 如果一个图的点连通度大于等于2，那么图是点双连通的，边双连通同理

  • 点双：不存在割点/任意两点之前存在至少两条点不重复的路径
    边双：不存在桥/任意两点之前存在至少两条边不重复的路径

  • 点双/边双联通分量：无向图的极大点双/边双联通子图

  • 割点将图分割成若干个点双，桥将图分成若干个边双 桥不属于任何边双，割点属于与其相连的

前置芝士

  1. DFS树：对图进行DFS时删去所有未经过的边产生的树

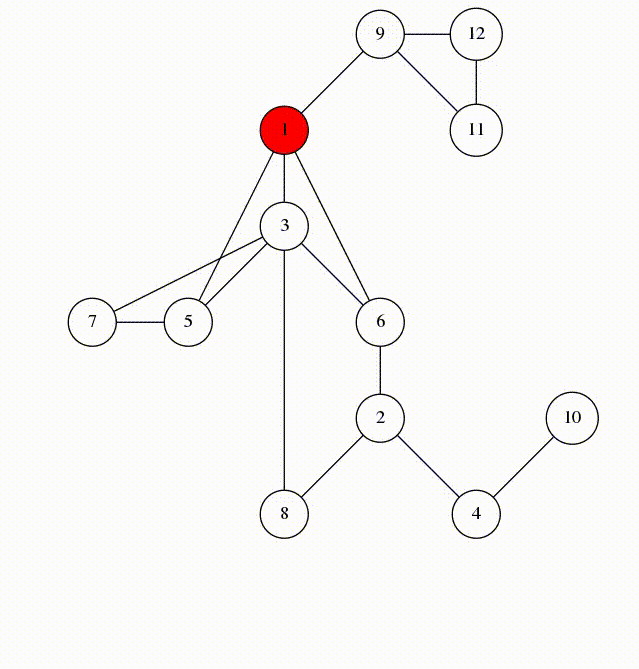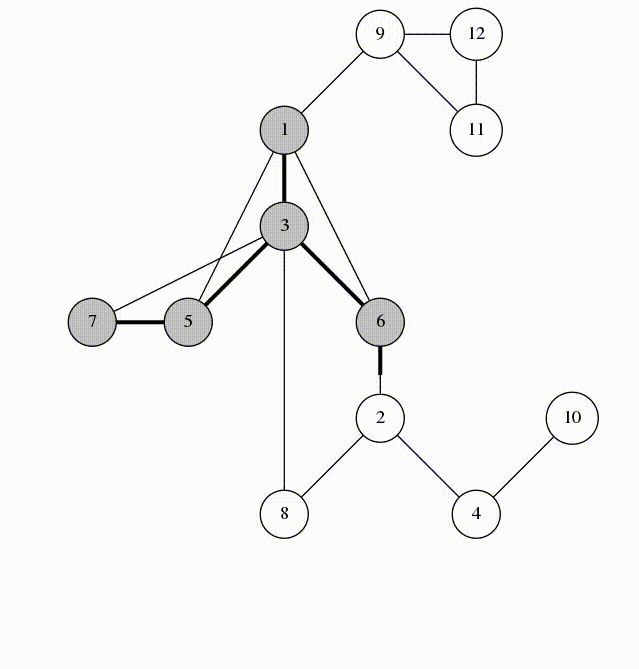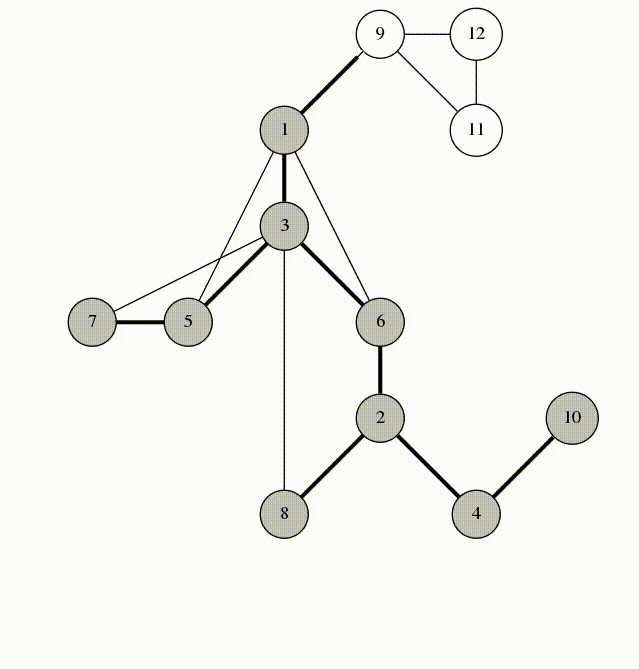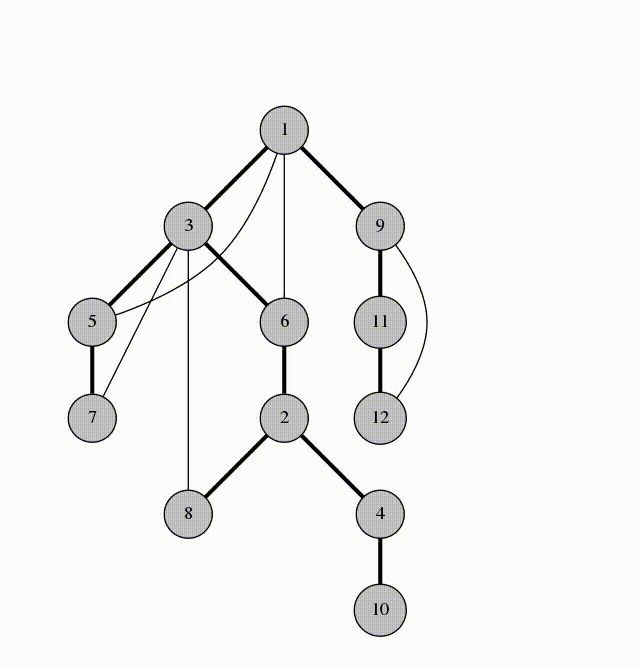
  2. DFS序：点被DFS的顺序

  3. 对于无向图，我们在树边与非树边之间进行区分

  4. 对于有向图，需要对边的分类进行进一步细化：

    1. 树边：DFS森林的实际组成部分
    2. 前向边：DFS树中从一个顶点指向该顶点 的一个非子顶点后裔的边
    3. 回边（返祖边）：DFS树中从一个顶点指向其祖先的边
    4. 横叉边：从一个顶点指向一个已完全访问过的顶点（即该顶点已经被最后一次访问）的边

用途

  1. 将复杂图上问题转化为相对简单的特殊图上问题
  2. 有向图找强连通分量（scc）、缩点（将强连通分量缩为一个点）
  3. 无向图找割点、桥

找强连通分量

  • 首先，我们需要

    1. 维护一个辅助栈，表示树根到当前点的节点序列

      用于找到 scc 后按遍历顺序倒序输出

    2. 维护两个标记，分别为

      1. dfn[u]，表示 $u$ 点在 DFS 序中的序号

      2. low[u]，表示 $u$ 点通过树边和至多一条连向当前强连通分量内部的非树边能访问到的dfn最小值

        即当前点可以到达的最先被访问的点

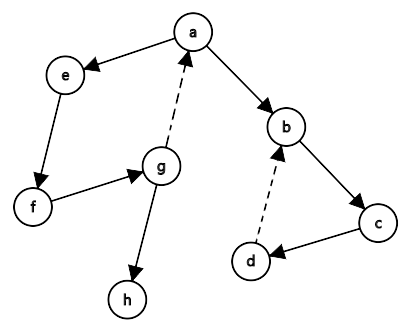
        如这张图，$b$ 点通过两条树边（$b \to c,c \to d$）和一条回边（$d\to b$）可以访问到的dfn最小值为 $b$

        因此 $\text{low}(b)=b$

  • 当一个点能访问到的最早的点为这个点本身（即 low 值等于 dfn 值），就会形成一个新的强连通分量

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
stack<int>s;
int ins[maxN];//记录点u是否在栈中
int dfn[maxN];
int low[maxN];

int cnt = 0;
int sccNum = 0;
int sccSiz[maxN];
int scc[maxN];

void tarjan(int u){
    cnt++;
    dfn[u] = cnt;
    low[u] = cnt;
    s.push(u);
    ins[u] = 1;
    for(int i = head[u];i;i = edge[i].nxt){
        int v = edge[i].to;
        //由于访问过的点一定被dfn标记过，所以可以通过dfn判断点v是否被访问过
        if(!dfn[v]){
            tarjan(v);
            //用下一个点的low值尝试更新当前点的low值
            low[u] = min(low[u],low[v]);
        }else if(ins[v]){
            //若曾经被访问过且在栈中，则这是一条回边
            //用下一个点的dfn值更新该点low值
            low[u] = min(low[u],dfn[v]);
        }
    }
    //若一个点的low值为dfn序，则该点为一个scc的始点
    if(low[u] == dfn[u]){
        ins[u] = 0;//准备出栈
        sccNum++;//记录数量
        scc[u] = sccNum;//点u是在第sccNum个scc中的点
        sccSiz[sccNum] = 1;//记录这个scc的大小
        while(s.top()!=u){
            int sT = s.top();
            scc[sT] = sccNum;
            ins[sT] = 0;
            sccSiz[sccNum]++;
            s.pop();
        }
        s.pop();//当前栈顶为该scc的最后一个点，将其出栈
    }
    return;
}

缩点

  • 即将一个强连通分量缩为一个点

    比如上面的图可以被缩成三个点

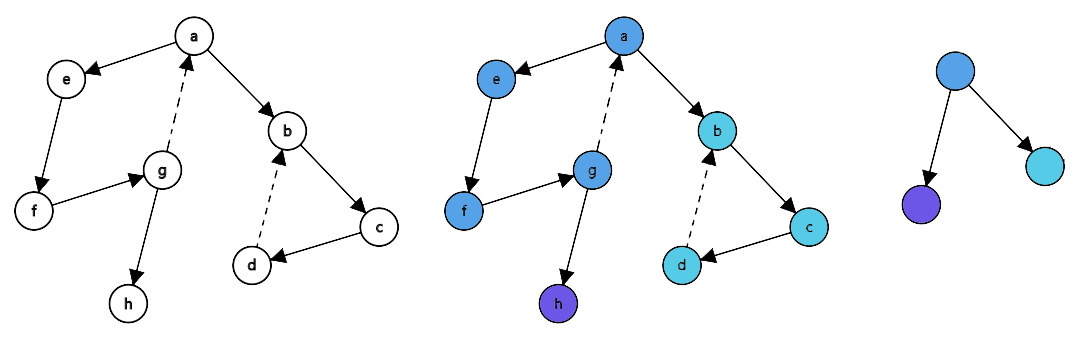
  • 由于在上面的代码中已经对每个点所属的 scc 进行了标注，标号相同的点就在同一个 scc 中，可以缩为一个点

  • 易知每一个出度大于1的点一定会连接其他的强连通分量，所以可以找到这种点，它可以到达的边中去掉到达同一个scc中的边，剩余的边即为到达其他scc的边，使用这些边重新建图

求割点、桥

  • 对于边 $(u,v)$，若 $low[v]>dfn[u]$，则 $(u,v)$ 是桥，若 $low[v]>=dfn[u]$ ，则 $u$ 是割点（只有一个儿子的根节点除外）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    //求割点
    void dfs(int u,int fa){
    	low[u] = dfn[u] = ++dfs_clock;
    	int c = 0;//记录孩子数
    	for(int i = head[u];i;i = edge[i].nxt){
    		int v = edge[i].to;
    		if(!dfn[u]){
    			dfs(v,u);
    			c++;
    			low[u] = min(low[u],low[v]);
    			if(low[v] >= dfn[u]) cut[u] = 1;
            }else if(dfn[v] < dfn[u] && v != fa){
    			low[u] = min(low[u],dfn[v]);
    		}
    	}
    	if(c == 1 && fa == 0) cut[u] = 0;//只有一个儿子的根节点除外
    }
    //求桥
    void dfs(int u,int fa){
    	low[u] = dfn[u] = ++dfs_clock;
    	for(int i = head[u];i;i = edge[i].nxt){
    		int v = edge[i].to;
    		if(!dfn[u]){
    			dfs(v,u);
    			low[u] = min(low[u],low[v]);
    			if(low[v] >=dfn[u]){
    				bcnt++;
    				bri[edge[i].id] = 1
    			}
    		}else if(dfn[v] < dfn[u] && v != fa){
    			low[u] = min(low[u],dfn[v]);
    		}
    	}
    }