最近公共祖先(LCA)
$\operatorname{lca}(u,v)$为点 $u$ 和 $v$ 的所有公共祖先中最深的一个
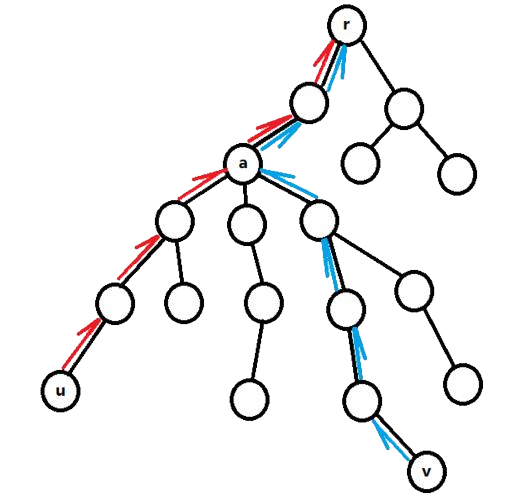
暴力跳父亲 $O(n)$
倍增 $O(n\log n)$预处理 $O(\log n)$ 查询
树链剖分 $O(n)$ 预处理 $O(\log n)$
$\operatorname{Tarjan}$ 均摊$O(1)$(离线)
$\operatorname{Rmq}$ $O(n \log n)$ 预处理,$O(1)$查询
倍增法
$f(i,j)$ 代表 $i$ 的 $2^j$ 级父亲
易知 $f(i,j)=f(f(i,j-1),j-1)$
即“ $i$ 的 $2^j$ 级父亲 为 $i$ 的 $2^{j-1}$ 级父亲的 $2^{j-1}$ 级父亲”( $ 2^j=2\times 2^{j-1}$ )
预处理
1
2
3
4
5
6for(int i = 1;i<=n;i++) f[i][0] = fa[i];
for(int j = 1;j<=20;j++){
for(int i = 1;i<=n;i++){
f[i][j] = f[f[i][j-1]][j-1];
}
}求 $\operatorname{lca}$
将 $u$ 和 $v$ 中较深的向上跳 $|\text{dep}_u-\text{dep}_v|$步,使他们的深度相同
如果此时 $u$ 和 $v$ 相等则返回
不断从大到小枚举 $i$ ,判断 $f(u,i)$ 和 $f(v,i)$ 是否相同,若相同就跳过头了,若不同则同时向上跳 $2^i$ 步
当然也可以从小到大枚举 $i$,寻找第一个可以使 $f(u,i)=f(v,i)$ 的 $i$,同时向上跳 $2^{i-1}$ 步
当 $f(u,0)=f(v,0)$时,答案即为 $f(u,0)$ 或 $f(v,0)$
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19int lca(int x,int y){
if(dep[x] < dep[y]) swap(x,y);//令x为较深的点
for(int i = 20;i>=0;i--){
if(dep[f[x][i]] >= dep[y]){
x = f[x][i];//如果跳完深度仍然深于另一个点,则向上跳2^i级
}
}
if(x == y) return x;//如果到达同一深度后两个点重合,则结果为较浅的点
for(int i = 20;i>=0;i--){
if(f[x][i] != f[y][i]){
x = f[x][i];
y = f[y][i];
//将两个点同时向上跳2^i步
}
}
return f[x][0];
}
树上dp
所谓树上dp,就是在树上进行的dp(经典废话
-
给一颗树,每个点有点权,选择一个连通块使得点权和最大
很明显这棵树中可能存在负权点,不然整棵树的权值和就是最大子树和
令 $f(i)$ 为以 $i$ 为根的连通块的最大子权和
易知 $f(i)=f(i)+\max(f(j),0)$ ,其中 $j$ 为 $i$ 的儿子
1
2
3
4
5
6
7
8
9void dfs(int fa,int x){
for(int i = head[x];i;i = edge[i].next){
int v = edge[i].to;
if(v == fa) continue;
dfs(x,v);
f[x] += max(f[v],0);
}
ans = max(ans,f[x]);
} -
给一棵树,要求选择一些点,满足任意点和他的父亲不同时被选的情况下点权和最大
令
$f(i,0)$ 为 以 $i$ 为根的子树且不选 $i$ 的最大点权和,
$f(i,1)$ 为 以 $i$ 为根的子树且选 $i$ 的最大点权和,
那么可以推出,
$f(i,0)=f(i,0)+\max(f(j,0),f(j,1))$,其中 $j$ 为 $i$ 的所有儿子
$f(i,1)=f(i,1)+f(j,0)$,其中 $j$ 为 $i$ 的所有儿子
$\text{ans}\gets \max(f(1,0),f(1,1))$
1
2
3
4
5
6
7
8
9
10
11void dfs(int fa,int x){
f[x][1] = val[x];
for(int i = head[x];i;i=edge[i].next){
int v = edge[i].to;
if(v == fa) continue;
dfs(x,v);
f[x][0] += max(f[v][1],f[v][0]);
f[x][1] += f[v][0];
}
}
int ans = max(f[1][0],f[1][1]); -
给定一棵树,要求在一些点上放置保安,保安可以看守该点即与该点相连的所有点,第 $i$ 个点放置保安有代价 $v_i$ ,求所有点都被看守的情况下的最小代价和
令
$f(i,0)$ 为以 $i$ 为根的子树,$i$ 被 $i$ 的父亲看守的最小代价和
$f(i,1)$ 为以 $i$ 为根的子树,$i$ 被 $i$ 他自己看守的最小代价和
$f(i,2)$ 为以 $i$ 为根的子树,$i$ 被 $i$ 的儿子看守的最小代价和
若一个点被其父亲看守,则该点无法看守其儿子节点,其儿子节点需要被【儿子自己】或【儿子的儿子】看守
即 $f(i,0)=f(i,0)+\min(f(j,1),f(j,2))$,其中 $j$ 为 $i$ 的儿子
若一个点被自己看守,则该点的儿子可以被【儿子自己】,【该点本身】,【儿子的儿子】看守
即 $f(i,1)=f(i,1)+\min(f(j,0),f(j,1),f(j,2))$
若一个点被其儿子看守,则其儿子节点可以被【儿子自己】,【儿子的儿子】看守,
即 $f(i,2)=f(i,2)+\min(f(j,1),f(j,2))$
但是如果转移方程仅仅是这样的话,当前节点可能没有人看守(即所有的儿子都由儿子的儿子看守时)
所以至少要有一个儿子是自己看守自己
不过如果出现这种情况,就表明所有的 $\min(f(j,1),f(j,2))$ 都是 $f(j,2)$ 更小一些
这时可以定义一个 $\text{tmp}$ 变量来记录 $f(i,1)$ 与 $f(i,2)$ 的差值,即定义 $\text{tmp}=f(i,1)-f(i,2)$
若 $\text{tmp} < 0$ 则说明 $f(i,1) < f(i,2)$ ,即出现了一个自己看管自己的儿子节点,就无须理会了
若 $\text{tmp} > 0$ 则说明当前的儿子节点是由儿子的儿子看管的,可以被修正为自己看管
而且当 $\text{tmp}$ 为正且越小的时候,说明将该儿子节点修改为自己看管亏损得越少
所以可以写出如下的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16void dfs(int fa,int x){
f[x][1] = val[x];
int tmp = 1e9;
for(int i = head[x];i;i=edge[i].next){
int v = edge[i].to;
if(v == fa) continue;
tmp = min(tmp,f[v][1]-f[v][2]);
f[x][0] += min(f[v][1],f[v][2]);
f[x][1] += min(min(f[v][0],f[v][1]),f[v][2]);
f[x][2] += min(f[v][1],f[v][2]);
}
f[x][2] += max(tmp,0);
//若tmp为正数则加上tmp起到修改作用
//f[j][2]+(f[j][1]-f[j][2])=f[j][1]
}
int ans = max(f[1][1],f[1][2]);
其他
又是亿些概念
- 树的重心:选一个点为根,使最大子树最小的点称为树的重心
- 树的直径:树上最长路径
- 树的中点:直径中点(树的中心不等于树的中心)
又是亿些性质
- 树直径可能有很多条,他们必定交于树的中心
- 树的中心是一个或两个
- 以树的重心为根是,所有子树的大小都不超过整棵树大小的一半
- 树的重心是一个或两个
- 两树相连,重心在原来两树重心的路径上